Kwadratische functies

Theorie

We gaan het vandaag hebben over kwadratische functies.
Voorbeelden van kwadratische functies zijn f(x)= x² - 7 en g(x)= x² +5x + 12

Bij kwadratische functies kun je verschillende functiewaardes uitrekenen. Dit kan je doen door de functie waarde in te voeren op de plek van de variabele. Bij het berekenen van functiewaarde -3 in de functie van g (bovenstaande functie) dan kan je dit als volgt noteren.
g(-3)= (-3)² + 5 · -3 + 12 = 9 - 15 + 12 = 6.
Dit lijkt heel erg op het invullen van een kwadratische formule. Het is belangrijk om te weten dat het rekenen met formules en functies op dezelfde wijze gaat, we noteren ze alleen op een andere manier.

formule: y= x² + 2x +8.
functievoorschrift: f(x)= x² + 2x + 8.

Voor nu gaan wij ons focussen op de meest standaard vorm van een kwadratische functie. Dat is; f(x) = ax²+ bx + c. Hierbij geldt wel dat a ≠ 0. Doordat we al veel weten van de kwadratische formules weten wij ook al veel van kwadratische functies.

De grafiek van een kwadratische functie heeft altijd dezelfde vorm. Namelijk die van een parabool.
Er zijn twee soorten parabolen, de bergparabool en een dalparabool. Bij het zien van de functie kunnen we gelijk zien welke van de twee het is.
Aan de van de a in de standaard functie kunnen we het herkennen. Bij een negatieve a is het een bergparabool, bij een positieve a is het een dalparabool. Je kan het onthouden door de denken aan smileys. Wanneer je blij bent, lach je veel. Daardoor lijkt je mond op een dalparabool. Wanneer je niet blij bent, kijk je vaak sip. Daardoor lijkt je mond op een bergparabool.

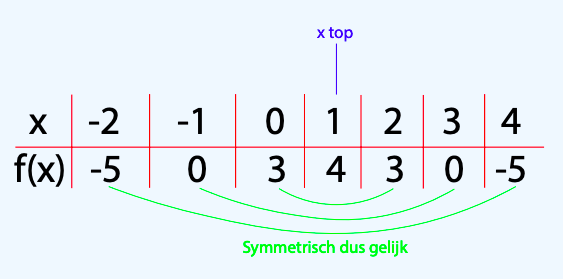
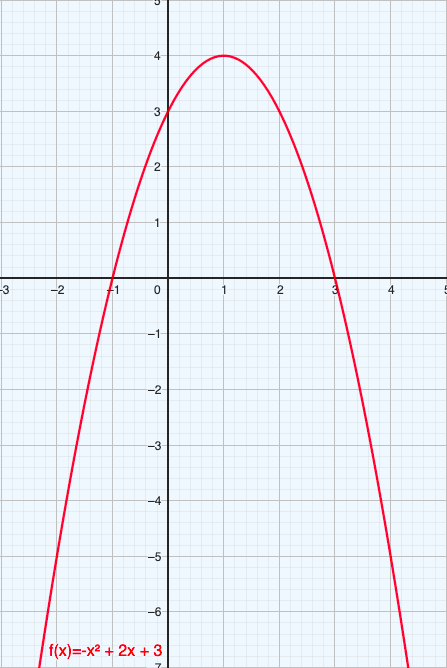
Parabolen zijn altijd symmetrisch. Daarbij valt de symmetrie-as samen met de x-coördinaat van de top. Deze informatie kan je gebruiken om een kwadratische functie te tekenen. We gaan de functie f(x)=-x²+ 2x + 3 tekenen.

We beginnen met het vinden van de top van de parabool. Later leren we een snelle manier om dit te kunnen doen, voor nu gaan we gebruik maken van twee functiewaarden die dezelfde uitkomsten hebben. In dit geval bijvoorbeeld f(0) en f(2) want;
f(0)= -0² + 2 · 0 + 3 = 0 + 0 + 3 = 3.
f(2)= -2² + 2 · 2 + 3 = -4 + 4 + 3 = 3.

Omdat de uitkomsten van de functiewaarden 0 en 2 gelijk zijn, weten we dat er symmetrie aanwezig is. Om de symmetrie as te vinden moeten we precies het midden zoeken tussen 0 en 2. Dat kunnen we doen door het gemiddelde te pakken van de functiewaarden.
xtop= ⁰⁺²/₂= 1

Nu we weten waar de top van de functie zich bevindt, kunnen we ook andere punten berekenen om de functie te tekenen.
In klas twee hebben we geleerd hoe we te werk moeten gaan. We maken als eerst een tabel waarbij we 7 punten moeten berekenen. Hierbij zorg je ervoor dat de top in het midden komt de staan. De top zit bij x=1 dus gaat onze tabel van x=-2 t/m x=4. Wanneer je de punten hebt berekent kan je deze tekenen in een assenstelsel. Let erop dat je de punten niet met een rechte lijn verbindt maar met een vloeiende kromme.