a(b+c)=ab+ac

Theorie

We gaan het hebben over de regel a(b+c)= ab + ac. Dit is een van de manieren om haakjes weg te werken.

Voor we naar de regel gaan kijken, gaan we eerst kijken naar een voorbeeld.

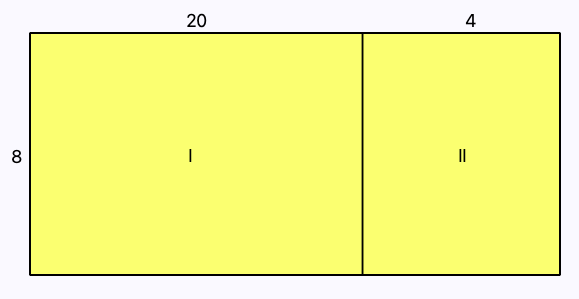
Hiernaast zie je een rechthoek, die verdeeld is in twee andere rechthoeken.
We weten een aantal afmetingen van dit rechthoek.
Bereken de oppervlakte van rechthoek.

Om de oppervlakte van een rechthoek te berekenen hebben we de formule
Oppervlakte rechthoek = lengte · breedte.
We gaan eerst de oppervlakte bereken van rechthoek I en vervolgens de oppervlakte van rechthoek II. Vervolgens kunnen we de oppervlakten bij elkaar optellen.
Oppervlakte I = 8 · 20 = 160
Oppervlakte II = 8 · 6 = 48
Totale oppervlakte= 160 + 48 = 208.

Wat je ook kan doen is eerst de lange zijde bij elkaar optellen. Daarna kan je de totale oppervlakte uitrekenen door de lengte met de breedte te vermenigvuldigen.
Oppervlakte= lengte · breedte, dus in ons voorbeeld;
Oppervlakte= 8(20+6). Onthoud goed dat tussen een getal en haakjes altijd een denkbeeldige · staat. We kunnen dit oplossen met behulp van de reken regels.
Oppervlakte= 8(20+6)=8 · 26 = 208.
We zien dat hetzelfde antwoord eruit komt.

Het principe van dit voorbeeld is de achtergrond van de regel die je goed moet kennen.
a(b+c)=ab+ac
Om haakjes weg te werken mag je altijd het getal voor de haakjes vermenigvuldigen met de beide getallen tussen haakjes.
zo is 2(x+4)= 2x + 8, want 2 ·x = 2x en 2 · 4 = 8

Je krijgt de volgende regel, waarbij elk boogje geldt voor vermenigvuldigen.